Logical Reasoning Tests: 2026 Guide for Logic Tests
Updated October 14, 2025
Logical reasoning tests measure a candidate’s problem-solving and logical reasoning skills in a wide variety of ways.
These logic tests are used in recruitment, particularly when assessing graduates for entry-level positions.
Logical reasoning tests may seem daunting and somewhat alien, but they use the same reasoning processes we rely upon daily – just in more overt and abstract ways.
As with any recruitment assessment, understanding exactly what the logic test involves and practicing similar questions will help to prepare you well.
What Are Logical Reasoning Tests?
Logical reasoning tests are a form of aptitude test commonly used during the recruitment process, especially in the corporate sector; investment banks, law firms, consultancies or accountancy firms, for example.
These logical aptitude tests aim to provide insight into your mental agility.
They most often require the interpretation and manipulation of statements, numbers, shapes and patterns.
The logical tests require the ability to calmly approach an abstract problem.
Questions will test candidates in a variety of ways but you may be asked to:
- Deduce trends
- Identify patterns
- Analyze arguments
- Draw conclusions
- Interpret relationships
- Identify flaws
Your score will display how quickly you can absorb and process new information and whether you have an aptitude for problem-solving and critical thinking.
Success in these tests is important, as it displays to a prospective employer that you are a deft candidate with a well-rounded mental capacity.
The name of the logical reasoning assessment you are presented with may vary depending upon the test provider.
The assessments may be referred to as logical reasoning tests, but may also be called inductive, abstract or diagrammatic reasoning tests.
There is overlap in the logical assessment test areas of these styles of questions and the overall principle remains the same.
If you are sitting a logical reasoning test, it is prudent to find out which company will be providing the assessment so you can get more of an idea of the kinds of questions that are most likely to appear.
Prepare for Any Job Assessment Test with JobTestPrep
Common Logical Reasoning Test Publishers
Common Logical Reasoning Test providers include:
- Talent Q
- Kenexa
- Saville
- Cubiks
- Revelian
- CAPP
- SHL
- Ravens
Logical reasoning tests may be used during the recruitment process for any position at any level but are most common for roles that have a significant problem-solving component and require high functioning logic.
They are most often encountered at the assessment center stage of the process but can also be used at the interview stage.
The Most Types of Logical Reasoning for the Logic Test
Diagrammatic Logical Reasoning
The most common type of logical reasoning test you will encounter is the diagrammatic form.
Simply put, you will be asked to answer questions based on shapes and patterns.
There will be a written question posed and then multiple-choice options to choose from for your answer.
These logic tests commonly test your abstract and inductive reasoning skills as they will assess your ability to identify patterns or trends and extrapolate or reapply this logic to select the correct diagram to complete a sequence (or identify the ones which don’t).
Verbal Logical Reasoning
Another common form of logical reasoning test is the verbal logical reasoning test.
This type of test is comprised of a series of paragraphs of text. Each will then have its own set of questions for you to work through.
Most commonly, the questions will consist of a list of statements.
You will then be required to decide which statement is the most accurate response, based on the information you have been given.
Some questions may present just one statement and require a choice between ‘Yes’, ‘No’ or ‘Cannot Say’.
These logic tests are looking at your deductive reasoning. You will be assessed on how well you can use the information given to come to logical conclusions.
This style of logical reasoning test requires active and attentive reading.
It is a good idea to ask yourself questions as you read to make sense of the scope and detail of what is covered in the text.
This will help you make judgments as to the validity of the statements in the subsequent questions more rapidly.
If you need to prepare for a number of different employment tests and want to outsmart the competition, choose a Premium Membership from JobTestPrep.
You will get access to three PrepPacks of your choice, from a database that covers all the major test providers and employers and tailored profession packs.
Practice Logical Reasoning Questions with JobTestPrep
Examples of Logical Reasoning Tests
Here you can find three example questions, similar to those you may encounter when taking a logical reasoning assessment:
Logical Reasoning Example 1
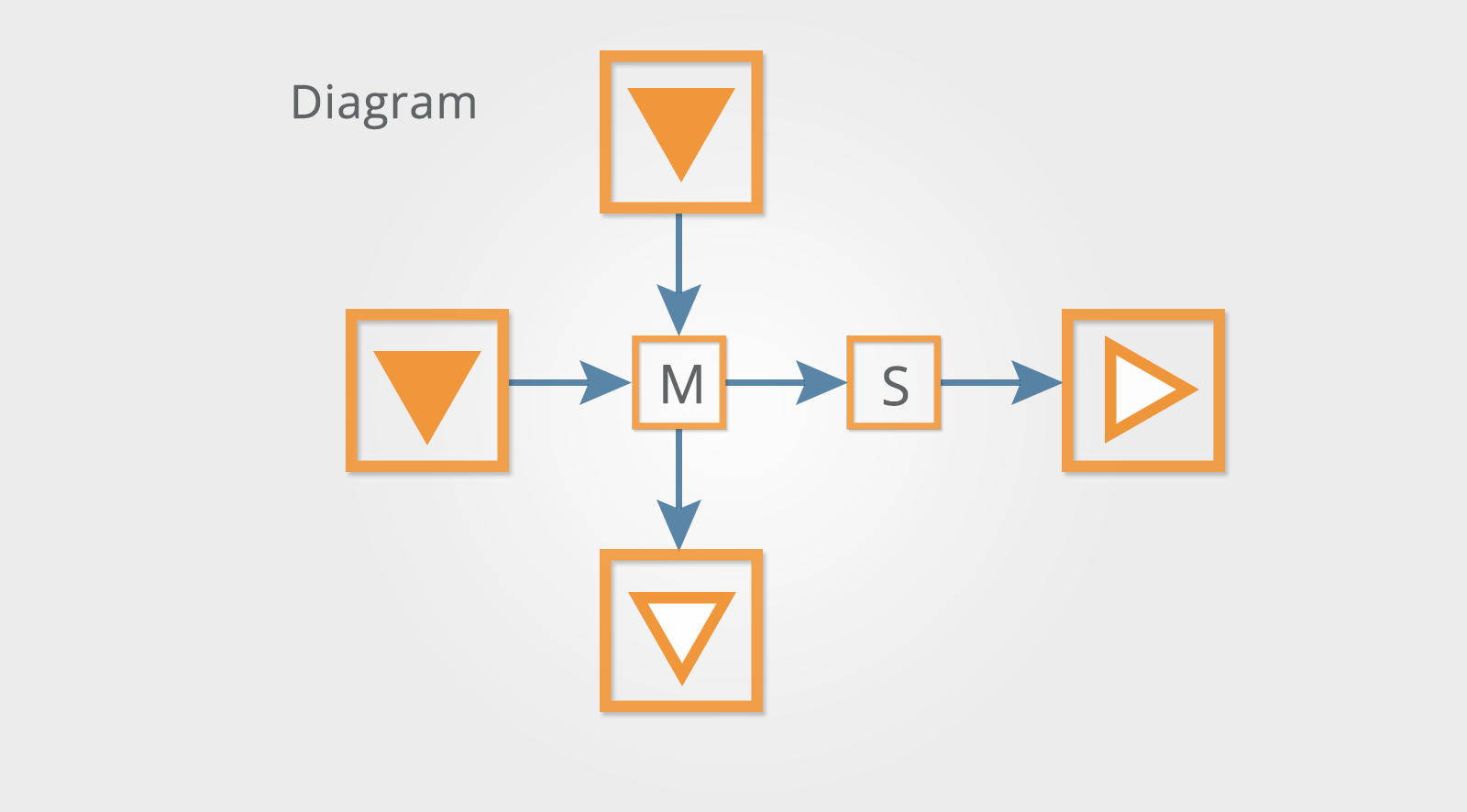

Look at the diagram above. In this process, the input shapes are being transformed by the functions 'M' and 'S'. Use the diagram to determine the effect each of these functions then apply them to the input shape in the question to arrive at the correct output.
Prepare for Any Job Assessment Test with JobTestPrep
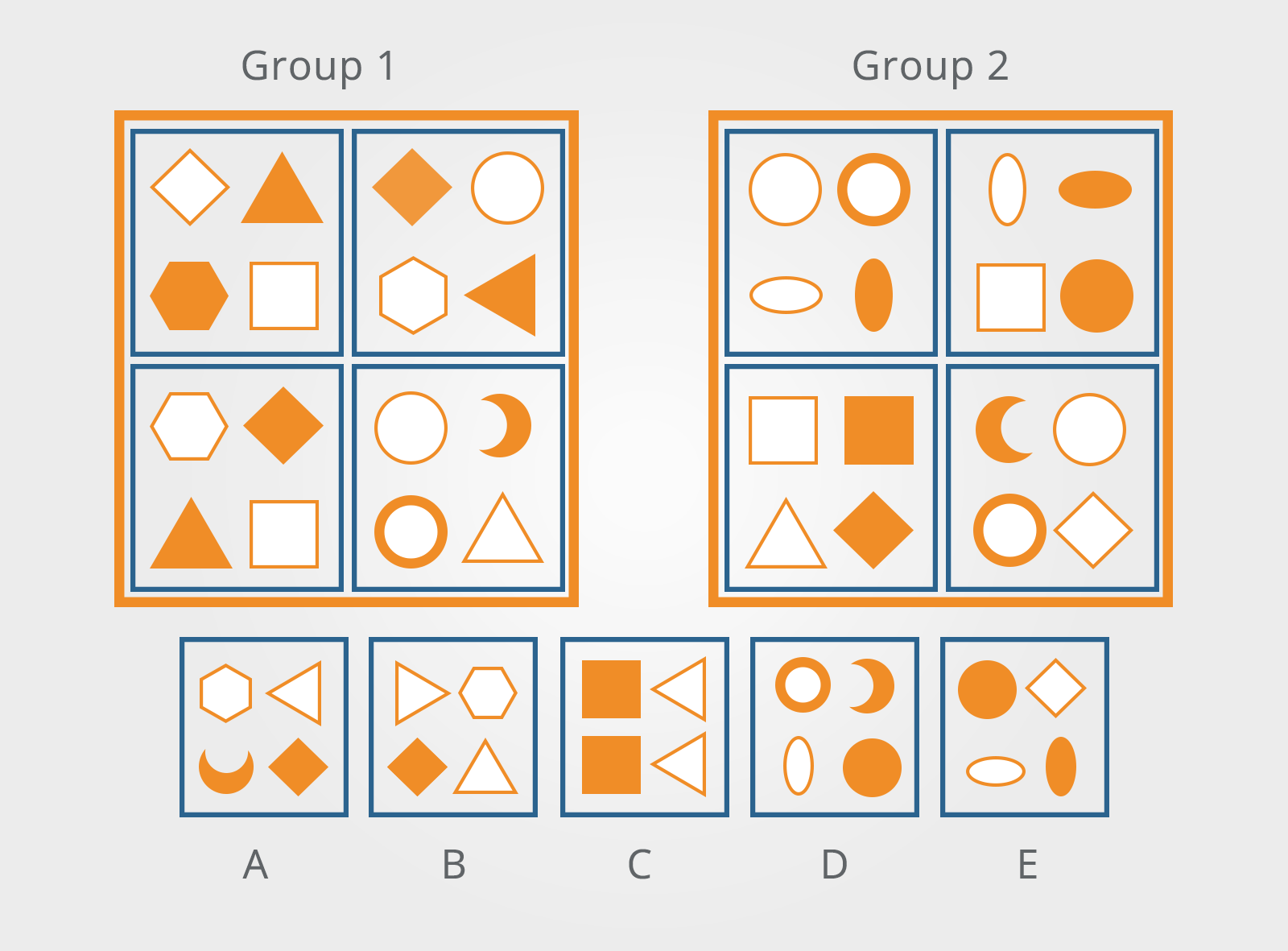
Which of the answer figures below belong in neither Group 1 nor Group 2?
Before you write down your answers, just double-check what the question was asking you.
It may seem obvious, but it is easy to misread ‘neither’ and answer the opposite question.
After spending time deducing the way the shapes in the patterns presented are governed, it would be galling to lose points because, when under time pressure, you accidentally answered the inverted question.
Logical Reasoning Example 3
Assuming the premises in the following text are true, what can we say about the conclusion drawn?
- Some employees of the cybersecurity company only drink coffee.
- Some employees only drink tea.
- Some drink both tea and coffee depending on the day.
- Some employees bring lunches.
- Some eat their lunches at their desk, whilst drinking coffee.
- Some never eat lunch at their desks.
There are some employees of the cybersecurity company who only drink coffee and never eat lunch at their desks.
Is the conclusion:
A) True
B) False
C) Uncertain
6 Logical Reasoning Tips to Prepare for Logic Tests in 2026
Step 1. Find Out Which Type of Test Your Prospective Employer Is Using
Before you begin to prepare for your logical reasoning test, confirm the type of test your prospective employer is using. Don’t be afraid to ask, as the term ‘logical reasoning’ can encompass many types of test.
Step 2. Practice Diagrammatic and Verbal Logical Reasoning
It is best to practice with questions closest to those you will encounter in the assessment, so trying to narrow down the question style is prudent.
If, however, you are unable to gain any further information on the test style, be sure to practice both the diagrammatic and verbal logical reasoning style of questions.
Step 3. Work Out the Answer Before Looking at the Answer Options
Attempt to work out what the correct answer, rule or sequence is before looking at the answer options.
This means that your logic will not be influenced by any of the possible answers.
It also ensures you double-check the logic of your answer upon viewing the options for selection.
Step 4. Start With the Answer
If you find yourself struggling to get to the correct answer in your practice sessions, work through some of the questions backward.
Look at the correct answer and then figure out what rule/pattern/evidence led to that answer.
This way, you will get used to working through the process of logic common in the questions.
Step 5. Practice Under Timed Conditions
When you are practicing logical reasoning questions, make sure you time yourself.
Sometimes, logical reasoning tests have strict time limits, so being aware of how long you might have for each question will help you when you are under pressure on the test day.
Step 6. Relax
The more familiar you become with logical reasoning tests, their format and the logic behind them, the faster and more accurate you will become at answering them.
It is important to relax so that your brain can focus on correctly solving the problem.
Prepare for Any Job Assessment Test with JobTestPrep
Remember that, with adequate practice, you will be in a great position to showcase your logical reasoning skills, so be confident and you’ll be well on your way to success.
Logical reasoning tests assess a candidate's ability to solve problems logically. Problem-solving is an essential part of many roles, meaning that logical tests are often included as part of an employer's recruitment process.
There are a variety of types of logical reasoning tests, each focusing on assessing a different type of logic used in problem-solving.
The most common logic tests used by employers to determine a candidate's logical reasoning include inductive reasoning, abstract reasoning, diagrammatic reasoning, or verbal reasoning.
Practicing logical reasoning tests vital to ensure you perform to the best of your ability when sitting the actual test.
When you practice logical reasoning, find out what type of logical reasoning test you will be completing and practice questions closest to those you will be asked to sit. If in doubt, practicing diagrammatic reasoning and verbal logical reasoning tests will help you understand the format and type of questions.
When sitting practice logic tests, make sure you time yourself to simulate the time pressure you will feel when taking the test itself.
Employers use several different test providers to administer Logical reasoning tests. These include SHL, Revelian, Talent Q and Kenexa.
Practicing logical reasoning tests is an important part of your preparation. The Psychometric Success website and app have many practice logical assessments tests that help you understand the format and style of questioning for each type of logical reasoning test.
You can find the Psychometric Success is available on Apple and Android devices.
Preparation is essential in ensuring you perform to the best of your ability when sitting a Logical reasoning test. Make sure you practice as many types of logical reasoning tests, including the kind that you are most likely to encounter in the actual test.
When practicing, do so under timed conditions to experience the time pressure you will face when it comes to sitting the actual test.
When faced with a question, try and work out the rule, pattern, or sequence before looking at the multiple-choice answers.
If you are struggling in the test, try and remain calm. If you are unsure of an answer, mark your best choice, then move on to the next question.
A Logical reasoning test is an objective way of assessing your logical reasoning ability when solving problems.
When used along with the information gained from all parts of the recruitment process, it provides a reliable way to predict whether candidates demonstrate the logical ability required for success in a role.
As problem-solving is a requirement for the job, logical reasoning tests are popular in the recruitment process for many graduate-level roles.
Preparation is vital. There are different types of Logical reasoning tests that employers use, such as diagrammatic reasoning, inductive reasoning, or verbal logical reasoning. Knowing which type of test you will be asked is important to ensure you practice the questions you are likely to be presented within the actual test.
Practicing these questions under timed conditions means you become used to how the question is formatted and how you react under time pressure. When sitting the test, try and remain calm, read the question and approach each question in a positive frame of mind.
When you start the test, make sure you are clear on the time limit for the test, this gives you the best opportunity to answer as many questions correctly as possible.
When tackling the questions, try and identify the pattern or rule before selecting your answer. Don't dwell too long on a question if you are struggling. Make an educated guess, then move on to the next question.
Practicing logical reasoning tests is an integral part of your preparation.
Becoming familiar with the format, style of questioning, and how you react under time pressure can help you perform to the best of your ability in the actual test.
For practice tests and free tips and advice on approaching and passing a logical reasoning test, visit the Psychometric Success website.
Employers use various types of Logical reasoning tests to assess your logical reasoning and problem-solving abilities.
When practicing logical reasoning tests, it is crucial to practice questions similar to those you will encounter in the ones you will sit.
The Psychometric Success app has lots of free advice, hints, and tips to help you prepare for any logical reasoning test.
The psychometric Success app is available on Android devices and is a valuable resource to prepare for and practice logical reasoning test questions.
There are many different logical reasoning tests, each assessing different kinds of logical reasoning and critical thinking.
When practicing logical reasoning tests, ensure you know the type of logical reasoning assessment you will be asked to sit as part of an employer's recruitment process.
Logical reasoning tests are assessments used by many employers for graduate-level vacancies. These tests assess your approach to problem-solving and whether you can evaluate information logically to reach a solution.
There are several logical reasoning tests, each assessing a different logical reasoning approach to problem-solving. These include diagrammatic reasoning, inductive reasoning, and abstract reasoning tests. When preparing for a logical reasoning test, it is helpful to understand what type of test you will be asked to sit.
If you are unable to determine which type of test you will be sitting it is advisable to practice diagrammatic reasoning and verbal logical reasoning tests as part of your preparation.
The benchmark that indicates a good score in a Logical reasoning test varies by employer. To ensure you perform at your best, showcase your logical reasoning abilities and attain a good score, it is essential to practice the tests.
When practicing, simulate test conditions by timing yourself and keeping to the recommended time duration of the test.
When sitting the test itself, remain calm, identify the rule or pattern in the information given before looking at the answer, and don't lose confidence if you find the assessment challenging.
Logical reasoning tests are used in the recruitment process for many graduate-level roles. These tests assess a candidate's ability to solve problems logically, an essential ability required for many positions.
There are several types of logical reasoning tests that employers use. Each employer will have its own criteria for assessing and scoring a logical reasoning test.
Understanding the type of logical reasoning test, you will be asked to sit, preparing through practicing tests, and when sitting the test remaining calm can all help you showcase your aptitude for logical reasoning.





