How to Calculate Fractions: A Step-By-Step Guide

What Are Fractions?

Fractions are numerical quantities that represent values of less than one. Also known as fractional numbers, they are commonly used to measure parts of a whole, such as:

• One half (1/2)
• One fifth (1/5)
• Two thirds (2/3)

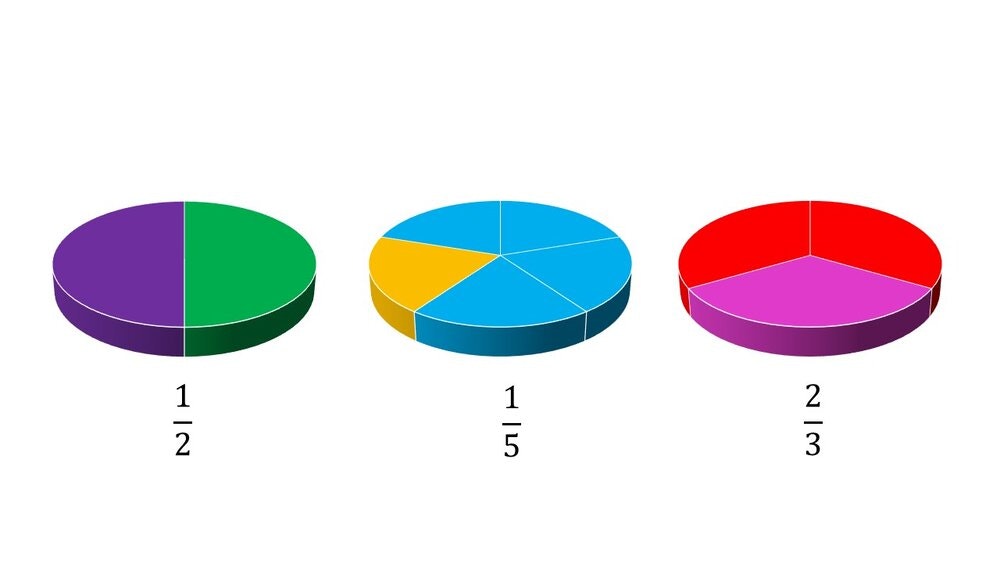
Fractions are made up of two numbers, one above and one below a dividing line.

The bottom number is known as the denominator and refers to the separate parts of the whole.

When we talk about the denominator, we use ordinal numbers – that is, numbers that define a position, like ‘third’ or ‘fourth’.

The top number of a fraction is called the numerator and refers to how many parts of the whole we are dealing with.

The simplest way to define a fraction is to imagine a pie that is equally divided into six pieces.

The pie itself is the whole and the individual slices are the parts of the whole. Since we have six equal parts of one whole, our denominator here is 6.

If we take one slice of the pie, we have one-sixth (1/6). Two slices are the equivalent of two-sixths (2/6) and so on.

This in itself is fairly simple to understand. However, there are different types of fractions and different methods for performing each type of fractional equation.

Key Fraction Facts

To understand how to work out fractions, it’s important to get to grips with the fundamentals. First, let’s look at the three different types of fractions:

Fraction Definitions and Examples

• Proper fraction – A proper fraction is a fraction in which the numerator is of lesser value than the denominator. 1/2, 10/15, and 85/100 are all examples of proper fractions. The overall value of a proper fraction is always less than one.

• Improper fraction – In an improper fraction, the value of the numerator is greater than that of the denominator. 6/3, 25/18 and 50/20 are all examples of improper fractions. The overall value of an improper fraction is always more than one.

• Mixed fractions – A mixed fraction is presented as a whole number followed by a fractional number, such as 2⅔, 6⅘ or 25⅝. Mixed fractions are also known as mixed numbers.

Key Terms

Now we know the different types of fractions, let’s look at some other key terms and phrases:

• Equivalent fractions – These are fractions that appear different but hold the same value. For example, 2/3 is the same as 4/6.

• Simplified fractions – These are fractions reduced to their lowest form. Basically, a lower equivalent of a higher fraction. So, using the example above, 2/3 is a simplified version of 4/6.

• Reciprocals – This is where the fraction is reversed by placing the denominator above the numerator. As an example, the reciprocal of 2/3 is 3/2. Reciprocals are used when dividing and multiplying fractions (5 ÷ 1/5 is the same as 5 x 5/1 or 5 x 5).

Fractions can also be presented as decimals and percentages. We’ll look at how to convert fractions in the example equations below.

10 Simple Fraction Problems and How to Solve Them

Below are ten examples of fractional equations and guidance on how to solve them. If you’re working with fractions in an exam setting, always be sure to show your method.

1. How to Convert a Mixed Fraction to an Improper Fraction

As discussed, a mixed fraction consists of a whole number followed by a fractional number. In this example, we’ll use the mixed fraction of seven and four-fifths, written numerically as 7⅘.

When asked to convert a mixed fraction to an improper fraction:

• First, multiply the whole number by the denominator of the fractional part.
• Take the resulting figure and add it to the fraction’s numerator.
• Take this final figure as your new numerator and place it over the original denominator. This gives you your improper fraction.

Example:

2. How to Convert a Fraction to a Decimal

Since both are used to identify values of less than one, a decimal is just a different way of representing a fraction.

The method used to convert a fraction to a decimal is a simple division: you just divide the numerator by the denominator.

Example:

3. How to Convert a Fraction to a Percentage

There are three easy ways to convert a fraction to a percentage. We’ll cover them all here using the same fraction of 7/20.

Method One:

Divide the numerator by the denominator, then multiply the resulting figure by 100 to get the percentage conversion:

7 ÷ 20 = 0.35

0.35 x 100 = 35%

Method Two:

Multiply the numerator by 100, then divide the resulting figure by the denominator:

7 x 100 = 700

700 ÷ 20 = 35%

Method Three:

Divide the numerator by the denominator and move the decimal point of your answer two places to the right:

7 ÷ 20 = 0.35

Moving the decimal point gives you the conversion of 35%.

When converting a fraction to a percentage, always remember to include the % sign in your answer.

4. How to Add Fractions

The process for adding fractions is straightforward provided the denominators are the same.

As a basic example, take 1/6 + 3/6. In this case, you have equal denominators, so simply add the numerators of both fractions, sticking with the lower figure of 6:

1 + 3 = 4

So, 1/6 + 3/6 = 4/6

When adding fractions where the lower figures don’t tally, you’ll first need to find the lowest common denominator. This is the lowest number wholly divisible by both existing denominators.

Example:

5. How to Subtract Fractions

As with addition, subtracting fractions is easy when the denominators are the same. It’s simply a matter of subtracting the second numerator from the first, keeping the bottom number the same.

Example:

Now, let’s look at subtracting fractions with different denominators.

Example:

6. How to Divide Fractions

To divide one fraction by another, you first need to turn the dividing fraction into a reciprocal by switching the denominator and the numerator.

Example:

7. How to Multiply Fractions

The process of how to work out fractions as multiplications of each other is a simple one:

• Multiply your numerators
• Multiply your denominators
• Write your new numerator over your new denominator

Example:

8. How to Simplify a Fraction

To simplify a fraction is to reduce it to its most basic form. Essentially, to find the lowest equivalent fraction possible.

First, find the greatest common factor. This is the highest whole number by which both numerator and denominator are divisible.

To do this, write down all the factors for both parts of your fraction, as shown below using the example of 32/48:

When completing any form of fractional equation, always simplify your answer to the lowest possible form.

9. How to Work out Fractions of Quantities

When presented with a quantity and asked to work out a fractional portion, simply divide the given amount by the fraction’s denominator, then multiply this figure by the numerator.

Example:

10. How to Determine Equivalent Fractions

To determine if one fraction is equivalent to another, either multiply or divide both parts of one fraction by the same whole number.

If your answers are also both whole numbers, then the fraction keeps its value and is equivalent.

Example:

You can also do this in reverse, multiplying both parts of the lower fraction:

4 x 3 = 12
5 x 3 = 15

Essentially, if one fraction is a simplified version of another, then they are equivalent.

Summary

Fractions are numerical quantities that help us measure equal parts of a whole.

They come in the form of proper, improper and mixed fractions, and can be easily converted into decimal points and percentages.

The methods used in fractional equations differ depending on the problem you are solving and each must be practiced with care, making sure you fully understand the question and showing your workings as you go.

Although they can seem daunting at first, taking the time to understand the basic rules should help you master how to work out fractions with ease.